Rozhliadli ste sa po dome a zistili ste, že potrebujete kúpiť veľa vecí. Napísali ste si dlhý zoznam, a musíte navštíviť veľký počet obchodov. Chceli by ste minimalizovať precestovanú vzdialenosť, aby ste si kúpili všetky veci.

Vaše mesto je organizované v sieti križovatiek a ciest medzi nimi. Váš dom a každý z obchodov, ktoré potrebujete navštíviť sa nachádzajú na nejakej z križovatiek. Vašou úlohou je nájsť najkratšiu cestu takú, že začína z vášho domu navštívi každý z obchodov do ktorých musíte ísť a vráti sa naspať domov.

Napíšte program, ktorý spracuje túto úlohu zadanú na štandardnom vstupe. Prvý riadok štandardného vstupu obsahuje dve čísla N (počet križovatiek) a M (počet ciest medzi križovatkami). N a M sú najviac 100 000. Križovatky sú číslované od 0 do N-1. Váš dom je na križovatke 0. Nasleduje M riadkov, na každom z nich sú tri čísla X, Y a D ktoré opisujú cestu z križovatky X do Y a dĺžkou D. Nasledujúci riadok obsahuje jedno číslo S – počet obchodov, ktoré chcete navštíviť. Nasleduje S riadkov, v každom sa nachádza jedno číslo označujúce obchod, ktorý chcete navštíviť. Počet obchodov S je najviac desať. Na štandardný výstup vypíšte jediné číslo – dĺžku najkratšej nákupnej cesty z domu navštíviac všetky obchody a návratom domov.

Zadanie pojednáva o „probléme obchodného cestujúceho“. Vo svojej podstate ide o graf, ktorého vrcholmi sú križovatky a hranami medzi týmito vrcholmi sú cesty medzi týmito križovatkami. Na jednej z týchto križovatiek, označenej indexom „0“ sa nachádza náš dom, teda štart a zároveň aj cieľ našej cesty. Obchody, ktoré chceme navštíviť sa nachádzajú tiež na takýchto križovatkách a ich číslo koreluje s indexom križovatky.

Celá realizácia zadania sa skladá z troch častí. Prvom časťou je samotné načítanie zadaných parametrov a ich uloženie do nejakej štruktúry. V druhej časti je využitý verejne známy Dijkstrov algoritmus, ktorý slúži na vypočítanie, resp. nájdenie najkratšej cesty medzi jednotlivými vrcholmi grafu. Treťou časťou je nájdenie všetkých rôznych možností, ktorými máme možnosť navštíviť všetky obchody a vrátiť sa domov. Ide vlastne o matematické permutácie. Zároveň je vypočítava vzdialenosť pre jednotlivé permutácie. Následne je vybratá tá najkratšia cesta spomedzi všetkých týchto možností.

Prvou úlohou je vybrať štruktúru na zapisovanie grafu. V mojom prípade ide o klasický prípad, ktorý sa využíva v počítačových sieťach, čiže maticu v podobe dvojrozmerného poľa. Táto matica má rozmer N x N, kde N označuje počet vrcholov. Z toho vyplýva, že indexy matice predstavujú index vrcholu v grafe. Na priesečníku týchto dvoch indexov je zapísaná vzdialenosť medzi týmito vrcholmi v grafe. Na obrázku 1 je všeobecný zápis matice. Z obrázka vyplýva, že napríklad pre vrcholy „2“ a „3“ je hodnota vzdialenosti medzi týmito vrcholmi „a23“.

Obrázok 1 Všeobecný zápis matice

Druhým dôležitým algoritmom je v mojom prípade Dijkstrov algoritmus. Miesto neho sa dali použiť aj iné algoritmy, ktoré majú prakticky tú istú funkciu. Najznámejšie podobné algoritmy sú Floyd-Warshallov algoritmus a Bellman-Ford algoritmus. Podstata všetkých algoritmov je hľadanie najkratšej vzdialenosti medzi vrcholmi. Nevýhodou algoritmu Floyd-Warshall je jeho efektivita. Ide o tri (z toho dva vnorené) cykly, čím sa rapídne zvyšuje náročnosť na výpočet. Napriek tomu ide o veľmi jednoduchý algoritmus, ktorý sa bežne používa. Druhou alternatívou je algoritmus Bellman-Ford, ktorý má rovnakú efektivitu vypočítania ako Dijkstra. Jeho výhodou je možnosť použitia aj záporných hodnôt veľkostí hrán. Táto možnosť je však v našom prípade úplne zbytočná. Z toho dôvodu som sa rozhodol použiť Dijkstra algoritmus. Tieto algoritmy boli podrobne popísané na prednáškach, preto iba stručne zhrniem opis jeho vykonávania.

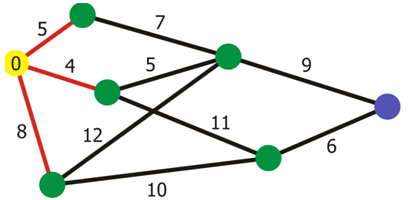
Obrázok 2 Dijkstra algoritmus

V prvom kroku zvolíme vrcholy, pre ktorý vzdialenosť budeme počítať. Pre počiatočný vrchol nájdeme všetky jeho hrany.

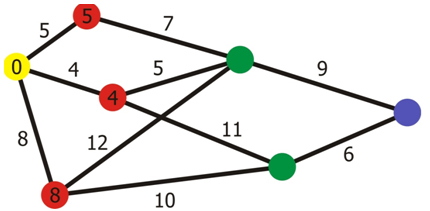
Obrázok 3 Dijkstra algoritmus

*Poznámka: Obrázok sa nachádza na tejto stránke. [5.12.2010]

Vrcholy ohodnotíme hodnotou cesty k vrcholom. Začneme hľadať najkratšiu cestu.

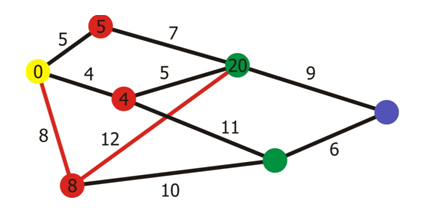
Obrázok 4 Dijkstra algoritmus

Ďalším krokom je nájsť cestu k vzdialenejšiemu vrcholu. Táto cesta môže mať niekoľko alternatív. Preto sa snažíme vybrať tú najkratšiu z možných ciest.

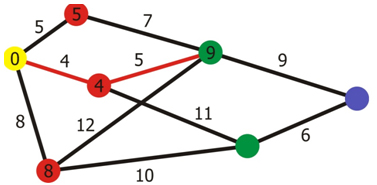
Obrázok 5 Dijkstra algoritmus

Toto opakujeme až pokým neprídeme ku konečnému vrcholu. Cesta medzi jednotlivými vrcholmi od počiatočného až po konečný predstavuje vzdialenosť medzi vrcholmi.

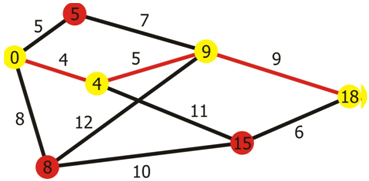
Obrázok 6 Dijkstra algoritmus

Ak sme našli všetky najkratšie vzdialenosti medzi zadanými vrcholmi, uložili sme ich do matice. Poslednou úlohou je nájsť najkratšiu cestu pre s pomedzi možných. Všetky možné cesty v princípe znamenajú všetky možnosti ako sa dajú navštíviť všetky dané obchody a vrátiť sa domov. Ide o matematické permutácie. Pri hľadaní týchto n-tíc si zároveň ukladáme hodnotu cesty. Nakoniec získame hodnotu pre jednotlivú permutáciu. Ak je táto hodnota menšia ako predchádzajúca hodnota najkratšej cesty, prepíšeme túto hodnotu. Toto vykonáme pre všetky permutácie. Nakoniec dostaneme v premennej cesta najkratšiu cestu spomedzi všetkých možných spôsobov.

Testovanie bolo za behu implementácie. Najprv som si vytvoril pár základných testov, ktorých úlohou bolo odhaliť základné chyby implementácie. Taktiež som využil metódu regresívneho testovania. Nakoniec som vytvoril väčšie scenáre na otestovanie programu pre otestovanie základných funkcií, rôznych výnimiek a podobne. Základné testy zbehli korektne a dávali správne výsledky. Väčšie testy trvali príliš dlho, hlavne z dôvodu použitia permutácií, ktoré pri veľkom počte zadaných prvkov sa vypočítavali nesmierne dlho. Keďže predpokladám, že na zbehnutie programu bude nastavený určitý limit, rozhodol som sa toto testovanie ignorovať.