

|

| |
|
Obr.2 - dekadické kódy |
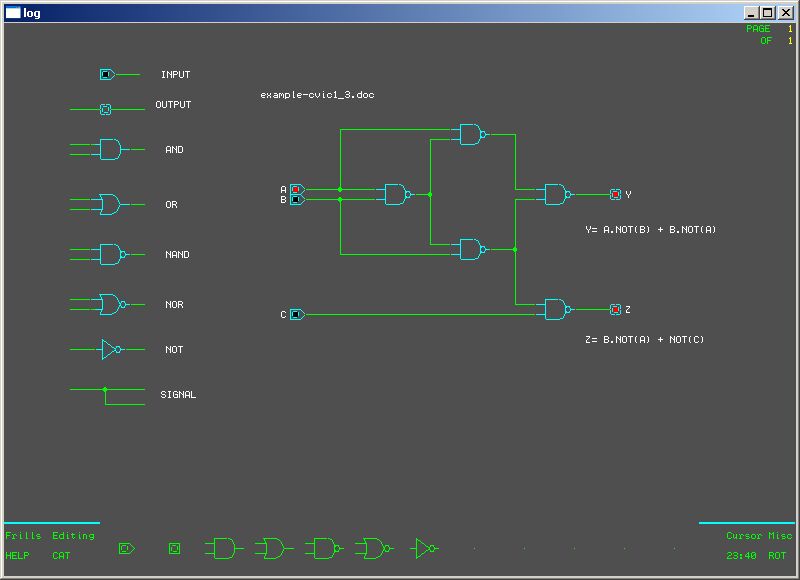
Obr.3 - Príklad, ako začať návrh |
|
Druhé zadanie je náročnejšie ako prvé zadanie, najmä čo sa týka nakreslenia schémy v simulátore LOG.
Odporúčame Vám preto Vaše schémy začať kresliť tak, ako to vidieť na obrázku 3: najskôr si pripraviť všetky vstupné signály
(aj ich negácie) a potom ich už napájať na NANDy tak, ako je potrebné.
Odporúčame pozrieť si aj schému nakreslenú k vzorovému riešeniu druhého zadania, kde je to takto nakreslené.
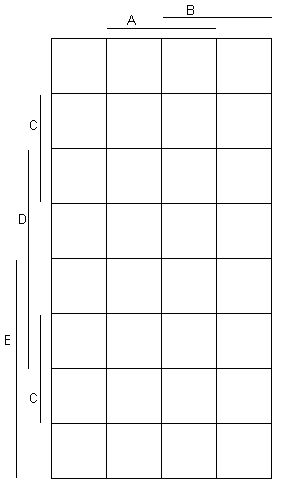
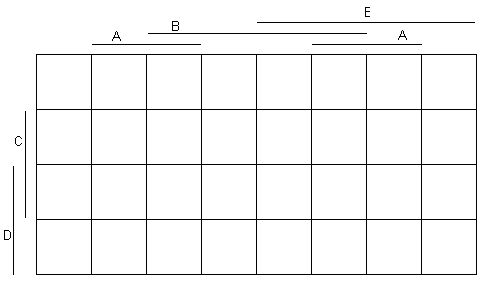
Musíte sami uznať, že výsledná schéma je prehľadná a nedá sa v nej pomýliť. Pre tých, ktorý potrebujú nakresliť karnaughovu mapu pre 5 premenných, budú nápomocné obrázky 4 a 5. |
| |
|
||
|
Obr.4 - Príklad karnaughovej mapy pre 5 premenných |
Obr.5 - Príklad karnaughovej mapy pre 5 premenných |
|
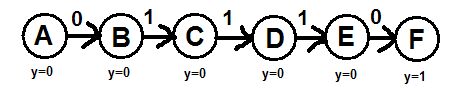
Najskôr je potrebné zostaviť stavový diagram. Jednotlivé stavy vyjadrujú, koľko správne rozpoznaných znakov sme našli v postupnosti,
pričom stav A vyjadruje žiadny správne rozpoznaný znak a stav F vyjadruje päť správne rozpoznaných znakov za sebou.
V našom prípade ide o postupnosť 01110. Najskôr si nakreslíme všetky stavy, ktoré môžu vzniknúť:
|
|
|
Obr.6 - stavový diagram, zobrazujúci stavy a prechody medzi nimi pri postupnosti 01110 |
|
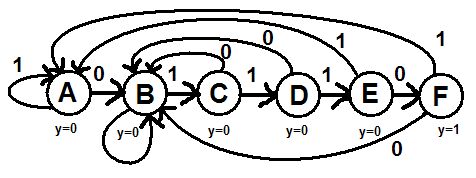
Čo ale robiť, ak rozpoznám iný znak, ako očakávam? V stave A je to veľmi jednoduché:
ak som nerozpoznal znak, ktorý by ma posunul do vyššieho stavu, ostávam v stave A čakať na ten znak(v našom prípade znak 0 nás posúva do vyššieho stavu, pri znaku 1 ostávame v stave A). Po vyriešení tohoto problému, sa nachádzame v stave B. Ak príde očakávaný znak 1, idem do stavu C. V prípade znaku 0 sa musím zamyslieť: Musím sa naspäť vrátiť do stavu A alebo môžem ostať v stave B? Ak by sme sa vrátili do stavu A, musíme čakať na znak 0, ktorý by nás posunul do stavu B. To je ale úplne zbytočné a nesprávne, pretože by sme sa nemohli posunúť do stavu C v prípade prijatia znaku 1. Musíme preto ostať v stave B, kde čakáme na znak 1. Sme v stave C. Čakáme na znak 1, ktorý nás posunie do stavu D. Príde nám ale znak 0. Čo teraz? Stav A, B alebo C? Povedzme, že sa vrátime do stavu A. Tu vzniká rovnaká situácia ako v predošlom prípade: na to, aby sme sa posunuli do stavu B, musíme získať ďalší znak 0 a to je nesprávne. Uvažujme teda stav C. V stave A sme rozpoznali 0, v stave B 1 a v stave C zase znak 0. Naša postupnosť je teda 010, my sme v stave C a očakávame 1. Po jej prijati by sme mali postupnosť 0101 a to nezodpovedá postupnosti, ktorú očakávame. Ostal teda stav B. V stave A sme prijali 0, v stave B 1 a v stave C zase 0. Máme postupnosť 010, čo taktiež nezodpovedá našej postupnosti, ale môžeme ísť do stavu B, pretože nulu, ktorú sme rozpoznali v stave C, by sme rozpoznali aj v A to je zbytočné. Ak ostaneme v stave B a ako ďalší znak rozpoznáme 1, dostaneme postupnosť 0101, čo síce nie je naša postupnosť, ale posledné dva znaky 01 tvoria začiatok novej postupnosti, ktorú môžeme rozpoznať. Takto pokračujeme až do konca, až nám vyjde stavový diagram, ktorý je nakreslený na obrázku č. 7. Tento diagram potom prekreslíme do stavovej tabuľky, ktorá sa nachádza aj v dokumente príkladu riešenia tohoto zadania 3. |
|
|
Obr.7 - hotový stavový diagram |
|
| Obr.8 - obvod zadaný FSM automatom |